AIは”浜田ゴリラ”を何と認識するのか？〜パーセプトロン編〜 │ Webty Staff Blog

どうも，こんにちは塚本です!

前回は，人工知能について簡単に解説をしましたが
今回からはDeep Learningについて詳しく踏み込んでいこうと思います．

今日のメインテーマはパーセプトロンです．

人工ニューラルネットワーク

わたしたち，人間の脳にはニューロンと呼ばれる神経細胞があり，
その伝達部分にはシナプスというものがあります．

人工ニューラルネットワークとは，その名の通りに，ざっくりいうと
脳の神経細胞の機能をコンピュータ上でシミュレーションしてやろうというものです．

ニューロンをモデル化した人工ニューロンと，それを繋ぐシナプスで構成されます．
重みを学習により変化させることで様々な計算を実現していきます．

特徴として，人工ニューラルネットワークは
入力層・出力層，そして中間層から構成されています．
（自分の論文からスクショしてきてるので図2とかこれから出てきますが順序はお気になさらず…）

じゃあ，人工ニューロンって，ざっくりどういうものなのか？
→　パーセプトロンに続きます．

パーセプトロンはフィードフォワード型の人工ニューラルネットワークの一つです．
1950〜1960年代にかけて，フランク・ローゼンブラットによって開発されました．

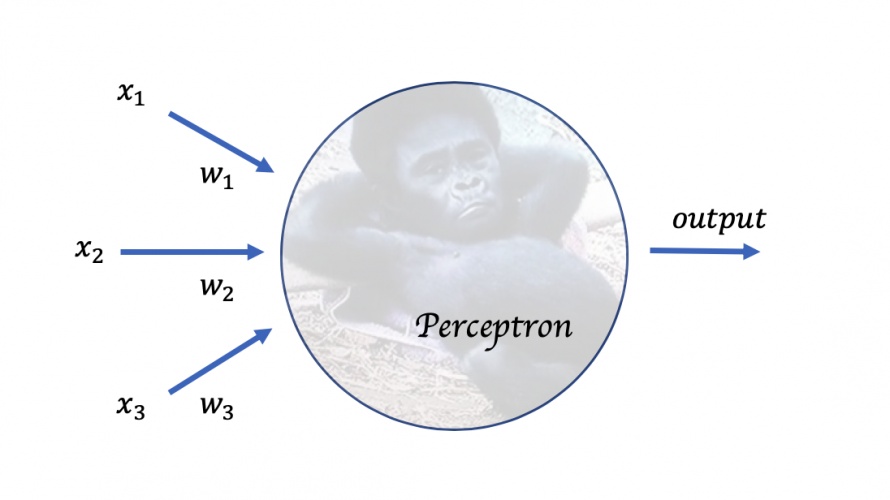
図3は単層パーセプトロンの基本構造になります．

パーセプトロンは複数の入力に対し，1つの2進数を出力します．
図3の例では，3つの入力x1,x2,x3が入っています．

ここで，出力outputを計算するルールとして”重み”という概念が登場します．
重み(w1,w2,w3)とは，それぞれの入力が出力に及ぼす影響の大きさを表すものであり，
出力は”入力の重み付きの和”と閾値の大小比較に決まります．

したがって，

このような数式(1)でパーセプトロンを表現することが可能です．

しかし，単層パーセプトロンでは線形分離不可能な問題は解けないという問題点があります．

線形分離とは，二次元平面上で2つの集合を1本の直線で分離できることをいいます．

こちらのサイトで詳しく説明されています．参考にしてください．
『線形分離可能ー単純パーセプトロンの限界 | ネジと銀』

単層パーセプトロンでは，線形分離不可能な問題は解けなかったので，
これを解決するために導入されたのが多層パーセプトロンになります．

単層パーセプトロンを”多層”に繋げたものになります．
多層パーセプトロンでは，シグモイド関数というものを使います．

シグモイド関数は”微分可能”で，
これを用いることによって多層ニューラルネットワークの学習を可能にしています．
(2)式がシグモイド関数の定義になります．

そして，シグモイド関数を用いたニューロンの出力は，ｚに先程の(1)式を代入し，バイアスを足した(3)式のような形をとります．

図4と図5に，シグモイド関数の概形と単位ステップ関数の概形を示します．
ちなみに図4ではf(x) = 1/(1+exp(-10x))を使用しています．

ここで，今までのお話のおさらいです．

パーセプトロンは複数の入力に対し，1つの"2進数"を出力します．

という話がありましたよね．
つまり，図5の単位ステップ関数は単層パーセプトロンの出力を指しています．

単位ステップ関数は，連続でない関数なので微分が出来ません．
ニューラルネットワークは学習する際に微分を用いて，重みを更新します．
ですので，単位ステップ関数では学習が続いていかないんですね．

それに対して，シグモイド関数はどうでしょうか？
単位ステップ関数によく似た形で，連続で滑らかです．
zの値(入力の重み付き和)によって傾きも変化し（正規分布に似た形にもなる）微分可能です．

そしてロジスティック回帰との関連性もあります．

シグモイド関数は"微分可能"で，
これを用いることによって多層ニューラルネットワークの学習を可能にしています．

最初の方で多層パーセプトロンについて，こう述べていたのはこういうことです．
そして，冒頭でみせた図2のニューラルネットワークの概要図というのが，多層パーセプトロンそのものになっています．

では，Deep Learningとはなんぞや…？
それは次回のブログにて☆