どうもこんにちは塚本です.
今週も,ブログネタが思いつかないので
コンデンサの話の続きをしたいと思います.
前回のブログでは,
かんたんに,なぜコンデンサがでんきを貯めることができるかを説明しました.
今回は,もう少し詳しく,それについて見ていきたいと思います.
静電容量

前回のブログでは,このような図を用いて平行平板コンデンサが電荷を保持する様子を示しました.
さて,この電荷達ですが
コンデンサはどこまで電荷達を保持し続けられるのでしょうか?
無限でしょうか?それとも,定員があるのでしょうか?
答えは,「定員」があります.
この「定員」のことを,静電容量[F]といいます.
静電容量C[F]
静電容量の記号はCで表します.
読み方はクーロンです.
由来は,物理学者のレジェンドであるシャルル・ド・クーロンから来ています.
そして,単位はFで表し,読み方はファラッドです.
由来は,電磁気界のレジェンドであるマイケル・ファラデーから来ています.
ファラデーの話は,またブログにしてみたいものです.
静電容量の公式
静電容量の大きさは,2つの金属板の大きさや間隔
絶縁体の種類によって決まってきます.
ここで,金属板の面積をS[m2],金属板間の距離をd[m],誘電率をε[F/m]とすると
平行平板コンデンサの静電容量C[F]は以下のように表すことが可能です.
C=εSd[F]⋯(1)
※ 誘電率とは,誘電分極のしやすさをいう定数です.
公式から見るコンデンサの性質
静電容量の公式を見て分かることとして,
金属板の面積が大きければ大きいほど,静電容量が大きくなることがわかります.
また,金属板の距離が広ければ広いほど,静電容量が小さくなります.
金属板の面積が大きいほど蓄えられる電荷の量が多そうですし,
距離が遠ければ遠いほど,プラスとマイナスのくっつきが弱そうですね.
とても直感的だと思います.
誘電率とはなんぞや?
静電容量の公式を紹介したときにサラッと書いている誘電率は何者なのでしょうか?
誘電率とは,媒体の分極のしやすさをいうものです.
ここで,分極のしやすさ=電気を蓄えられる大きさ と思ってもらえばOKです.
媒体とは,ここでいう金属板間に挟まれている絶縁体のことになります.
誘電分極

ここで,絶縁体について見ていきましょう.
絶縁体は,電気を流さない物質のことです.
電気が流れるということは,電子が移動するということです.
絶縁体は,内部の分子が規則正しく並んでおり,自由に移動できる電子がないもののことをいいます.
絶縁体に電圧をかけてみると…
少し難しい話になりますが,
絶縁体に電圧がかかるとき(=コンデンサに電気をながしたとき),
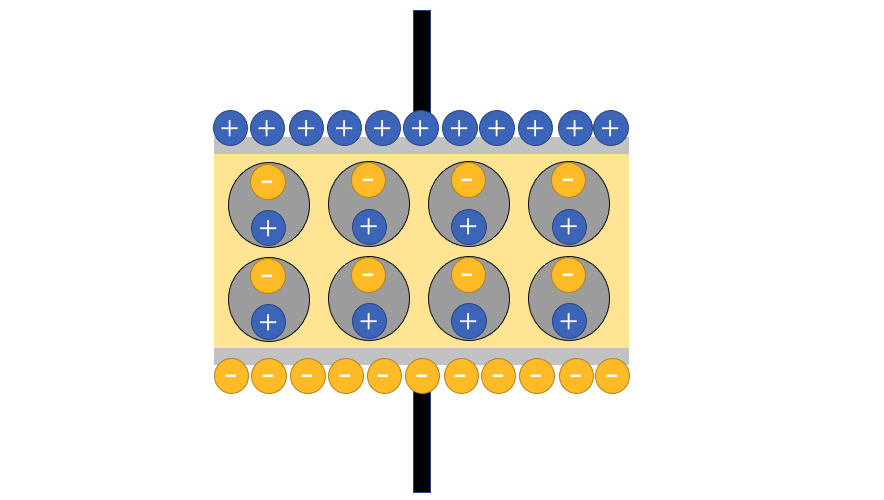
絶縁体の中の分子・原子内の電荷に以下のような偏りがおきます.

こうなると,隣接する分子間にはマイナスとプラスで,電気的に中性な状態が起きます.
つまり,以下の図の緑の丸の部分は電気的に中性な状態といえます.

電気的に中性ということは,以下の図の状態とみなすことが可能です.

見かけ上,電荷の定員が増えていると思います.
この増えた電荷のことを分極電荷と呼びます.
また,この現象を誘電分極 といい,誘電分極のしやすさを誘電率といいます.
つまり,誘電率が高ければ高いほど,電荷の定員が増えます.
かんたんにですが,こういったイメージです.
まとめ
本当は,真空の誘電率などの話までしたかったのですが
難しくなる&長くなるので今回はここまでとします.
なるべく,数式を用いず簡単なイメージ図で分かるように書いてみたつもりです.
コンデンサは面白いので,みなさんの興味をもつきっかけになってくれれば嬉しいです.

どうもこんにちは塚本です.
今週も,ブログネタが思いつかないので
コンデンサの話の続きをしたいと思います.
前回のブログでは,
かんたんに,なぜコンデンサがでんきを貯めることができるかを説明しました.
今回は,もう少し詳しく,それについて見ていきたいと思います.
静電容量
前回のブログでは,このような図を用いて平行平板コンデンサが電荷を保持する様子を示しました.
さて,この電荷達ですが
コンデンサはどこまで電荷達を保持し続けられるのでしょうか?
無限でしょうか?それとも,定員があるのでしょうか?
答えは,「定員」があります.
この「定員」のことを,
静電容量[F]といいます.静電容量C[F]
静電容量の記号は
Cで表します.読み方は
クーロンです.由来は,物理学者のレジェンドである
シャルル・ド・クーロンから来ています.そして,単位は
Fで表し,読み方はファラッドです.由来は,電磁気界のレジェンドである
マイケル・ファラデーから来ています.ファラデーの話は,またブログにしてみたいものです.
静電容量の公式
静電容量の大きさは,2つの金属板の大きさや間隔
絶縁体の種類によって決まってきます.
ここで,金属板の面積を
S[m2],金属板間の距離をd[m],誘電率をε[F/m]とすると平行平板コンデンサの静電容量
C[F]は以下のように表すことが可能です.C=εSd[F]⋯(1)
※ 誘電率とは,誘電分極のしやすさをいう定数です.
公式から見るコンデンサの性質
静電容量の公式を見て分かることとして,
金属板の面積が大きければ大きいほど,静電容量が大きくなることがわかります.
また,金属板の距離が広ければ広いほど,静電容量が小さくなります.
金属板の面積が大きいほど蓄えられる電荷の量が多そうですし,
距離が遠ければ遠いほど,プラスとマイナスのくっつきが弱そうですね.
とても直感的だと思います.
誘電率とはなんぞや?
静電容量の公式を紹介したときにサラッと書いている
誘電率は何者なのでしょうか?誘電率とは,媒体の分極のしやすさをいうものです.
ここで,分極のしやすさ=電気を蓄えられる大きさ と思ってもらえばOKです.
媒体とは,ここでいう金属板間に挟まれている絶縁体のことになります.
誘電分極
ここで,絶縁体について見ていきましょう.
絶縁体は,電気を流さない物質のことです.
電気が流れるということは,電子が移動するということです.
絶縁体は,内部の分子が規則正しく並んでおり,自由に移動できる電子がないもののことをいいます.
絶縁体に電圧をかけてみると…
少し難しい話になりますが,
絶縁体に電圧がかかるとき(=コンデンサに電気をながしたとき),
絶縁体の中の分子・原子内の電荷に以下のような偏りがおきます.
こうなると,隣接する分子間にはマイナスとプラスで,電気的に中性な状態が起きます.
つまり,以下の図の緑の丸の部分は電気的に中性な状態といえます.
電気的に中性ということは,以下の図の状態とみなすことが可能です.
見かけ上,電荷の定員が増えていると思います.
この増えた電荷のことを
分極電荷と呼びます.また,この現象を
誘電分極といい,誘電分極のしやすさを誘電率といいます.つまり,誘電率が高ければ高いほど,電荷の定員が増えます.
かんたんにですが,こういったイメージです.
まとめ
本当は,真空の誘電率などの話までしたかったのですが
難しくなる&長くなるので今回はここまでとします.
なるべく,数式を用いず簡単なイメージ図で分かるように書いてみたつもりです.
コンデンサは面白いので,みなさんの興味をもつきっかけになってくれれば嬉しいです.